Second Round Climate Data
In the IMAGE 2.2 model a simple climate model is used (the MAGICC model, developed at CRU Norwich by Tom Wigley and Sarah Raper) that calculates the global mean surface temperature change and given changes in the global radiative forcing. This results in one global estimate for climate change each year. For the pattern scaling to 0.5 by 0.5 degrees GCM climate patterns are used. Thus: the CRU database is applied for actual climate data (thirty-years mean over 1960-1990) and the pattern scaled climate change after 1990 is added, using different GCM patterns. Due to the fact that the differences in patterns of one GCM for the 20s, 50s and 80s is not as large as the differences of the patterns between different GCMs, here only the 50s pattern of each GCM is used for the pattern scaling (hence the thirty years mean of each GCM for the period 2035-2065). This approach is documented in the IPCC special report of Carter et al, 1994 (Carter, T.R., M.L. Parry, H. Harasawa and S. Nishioka, 1994. IPCC Technical Guidelines for Assessing Impacts of Climate Change. IPCC Special Report 0904813118. Intergovernmental Panel on Climate Change, WMO and UNEP, Geneva. pp 59.).
The GCM profile used for the pattern scaling is based on greenhouse gas forcings only. Since, sulfur aerosols do not act linearly on the climate system a delicate pattern scaling approach was implemented, based on regional GCM results from Schlesinger et al, (2000) to deal with the non-linear effects of sulfur aerosols (see below). (notes from Bas Eickhout; RIVM) .
Geographical Pattern Scaling (GPS)
The condition is that a GCM with a climate-change pattern due to changes in greenhouse gases only is used for the pattern scaling. If a GCM climate-change pattern is obtained by increased greenhouse gases and aerosols, the radiative forcings differ per hemisphere and per land or ocean. The division of the radiative forcings of aerosols over the four boxes is calculated with the following ratios (Wigley and Raper, 1992 and Raper et al., 1996):
- 4:1 for the direct forcing between northern and southern hemisphere;
- 2:1 for the indirect forcing between northern and southern hemisphere;
- 99:1 for the ozone forcing between the northern and southern hemisphere;
- 9:1 within each hemisphere between land and ocean for all of the three groups, mentioned above.
The climate-change patterns are not simulated explicitly in IMAGE 2.2. The global-mean surface temperature change, output of UDCM, needs to be linked to a monthly 0.5 x 0.5 degrees grid, considering the requirements of the Terrestrial Environment System of IMAGE 2.2. This linking is applied by using the standardized IPCC pattern-scaling approach (Carter et al., 1994).
In this approach, the General Circulation Model (GCM) results of a control
equilibrium climate are subtracted from the GCM results of an equilibrium
experiment climate (i.e., doubled CO2). This gives (monthly) geographical
distributions of experiment-induced equilibrium climate change (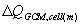 ).
The normalization of these GCM results is done by the corresponding change
in annual global-men surface temperature (
).
The normalization of these GCM results is done by the corresponding change
in annual global-men surface temperature (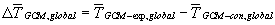 ).
Next, the global-mean surface temperature change from UDCM is used as
multiplicator to obtain the time-dependent geographical distributions
of climate change (per month) relative to the reference year (1990). Thus,
the global-mean surface temperature from UDCM is relative to 1990 as well.
In equation:
).
Next, the global-mean surface temperature change from UDCM is used as
multiplicator to obtain the time-dependent geographical distributions
of climate change (per month) relative to the reference year (1990). Thus,
the global-mean surface temperature from UDCM is relative to 1990 as well.
In equation:
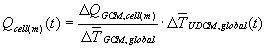 (1)
(1)
To obtain the absolute values, the monthly, observed climate data are added. In IMAGE 2.2, the observed data of the 1961-90 mean climate are used (New et al., 1999). This approach is well known and already implemented in IMAGE 2.1 (Alcamo et al., 1998).
This simple, computationally practicable approach is necessary because many uncertainties exist on the future emissions of greenhouse gases and SO2 and hence, it would be computationally impossible to perform a numerous of emission scenarios with a GCM to span the full range of possibilities. Furthermore, the sensitivity of the climate system and the forcing by the sulfate aerosols are highly uncertain. To assess the consequences of different climate sensitivities, UDCM can be used with different settings. To take the uncertainties in the forcing by sulfate aerosols into account, IMAGE 2.2 uses results from the AGC/MLO model (11-layer troposphere/lower-stratosphere general circulation/mixed-layer-ocean) from the University of Illinois at Urbana-Champaign (UIUC). The approach to take the non-linear effects of sulfate aerosols into account is introduced by Schlesinger et al. (2000).
The following steps are taken, according this approach:
- A first run of UDCM is based on the climate forcing after 1990 by greenhouse gases only. The corresponding climate change is scaled with a greenhouse gas-only pattern from a selected GCM (see equation 1). The Hadley GCM run with greenhouse gases only (HADCM2) is used as default in IMAGE 2.2.
- A second run of UDCM uses the climate forcing by sulfate only (other greenhouse gases held constant after 1990). The forcing is calculated as described in Harvey et al (1997). Only the corresponding temperature change is scaled with a sulfate-only pattern from the AGC/MLO model. The sulfate-only pattern is constructed with a 10xSO4 simulation by AGC/MLO. A 1xSO4 simulation is not used because the corresponding forcing (-0.55 W/m2) yields a change in the global-mean surface temperature that is not much larger than the year-to-year variability of the control simulation (Schlesinger et al., 2000). Schlesinger et al. (2000) show that it is justified to use the same climate sensitivity in UDCM for this run as for the greenhouse gases-only run. The results of the first and second run are added (no weights) to obtain the combined pattern of radiative forcings by greenhouse gases and sulfate aerosols.
- 3-8. So far, only linear responses are taken into account. Runs 3-8 are made to account for the non-linear climate response to radiative forcing by sulfate aerosols. These steps are only applied to the temperature change patterns of GCMs. There is too little known about cloud formation, to apply this method to precipitation patterns.
The assumption in this approach is that the response to sulfate forcing is almost linear. Hence, the sum of runs one and two almost represents the climate changes correctly. However, because of local climate circumstances, it matters globally whether SO2 emissions increase in, for example, China or in the USA. Thus, the increases of SO2 emissions in different world regions since 1990 are translated into global-mean changes in radiative forcing and are scaled with a specific climate change pattern. This specific climate change pattern is obtained by an experiment run with 10xSO4 forcing in those world regions. These climate change patterns stem from the AGC/MLO model. The AGC/MLO model has delivered sulfate-only results for 6 world regions. In Table 1, these 6 regions are compared with the IMAGE 2.2 regions that coincide with these regions. The weights of the 6 regional patterns are calculated as follows (Schlesinger et al., 2000):
- First, the regional sulfate burden in 1990 is calculated using regression equations presented by Schlesinger et al. (2000) relating the sulfate aerosol burden (mg/m2) and annual SO2 emissions (g/m2) for the six regions (i);
- The ratio gi of the sulfate burden in region i to the global sulfate aerosol burden is calculated for the year 1990 (no scenario dependency);
- The future ratios of regional to global sulfate burden are calculated for each scenario with the same regression equations. This gives time-dependent ratios fi,j;
- The weight factor di,j is calculated as follows: di,j = gi - fi,j;
- For years after 1990, the weight factor di,j is used to multiply the regional forcings, calculated from the emissions of SO2 in;
- The temperature changes from runs 3-8 are scaled with the six AGC/MLO patterns, constructed with increased forcings in the six UIUC regions;
- These six scaled temperature patterns are added to the combined pattern of the first two runs for forcing by greenhouse gases only and sulfate only. In this way the combination of the first two runs is corrected for the regional differences in forcing by future SO2 emissions (see equation 2; with i as index for the 6 UIUC regions).
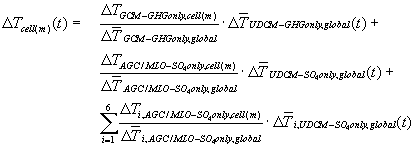 (2)
(2)
Table 1: The 6 world regions from UIUC (Schlesinger et al., 2000) compared with the 17 IMAGE 2.2 world regions (IMAGE team, 2001a)
| UIUC regions | IMAGE 2.2 regions |
| North America |
|
| North Africa |
|
| Europe |
|
| Siberia |
|
| Asia |
|
| Southern Hemisphere |
|
(Notes from Bas Eickhout; RIVM ) back